データサイエンスの勉強していると統計学の知識は欠かせません。
そこで、絶対に出てくる標準偏差や分散を理解するために正規分布の図が出てきますが、図を見ているだけでは理解つながりにくいです。
そこで、pythonで正規分布の図を作成して、標準偏差の値を変化させてみます。
それがどんな影響を与えるのかを確認することで、直感的な理解につながります。
pythonで作ると言いましたが、正確にはpythonのモジュールであるnumpyで作成します。
結論から言ってしまうと、正規分布に従う乱数を生成する関数であるnp.random.normalを使用します。
正規分布とは?
簡単に言ってしまうと、「ありふれた」「通常の」確率分布です。
様々な事象が下記のグラフのような左右対称な曲線になります。
特徴としては下記のものがあるので、これから試す方法を示すので是非試してみてください。
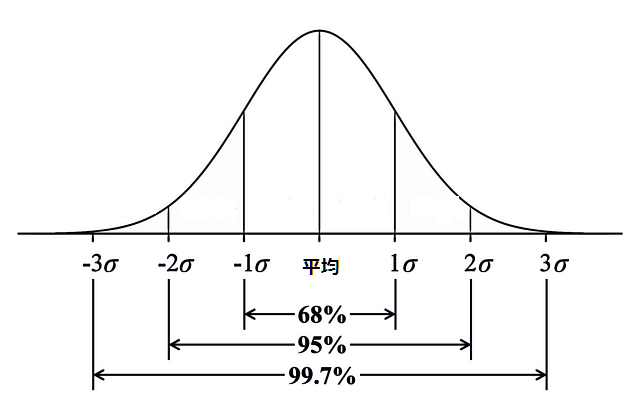
- 平均値と最頻値と中央値が一致する。
- 平均値を中心にして左右対称である。(直線x=μに関して対称)
- x軸が漸近線である。
- 分散(標準偏差)が大きくなると、曲線の山は低くなり、左右に広がって平らになる。分散(標準偏差)が小さくなると、山は高くなり、よりとんがった形になる。
np.random.normalで正規分布に従う乱数を作成
今回のコードはjupyter notebook上で行うことを想定したコードになります。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
incomes = np.random.normal(100.0, 20.0, 10000)
plt.hist(incomes, 50)
plt.show()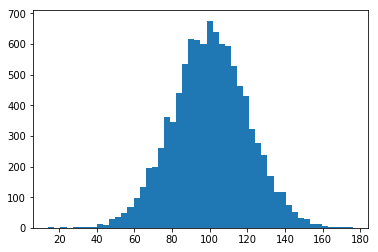
上記で示した画像と同じような図が描画されました。
肝となるコードは、np.random.normal(100.0, 20.0, 10000)です。
それぞれの引数が何を意味するかを理解すれば、色々と試すことができます。
一番最初の引数(100)が、平均を表し、2番目の引数(20.0)が、標準偏差を表します。
最後の引数が、何個の乱数を作成するかになります。
plt.hist(incomes, 50)の50を大き値に変更すると曲線が滑らかになるので、より最初の画像に近づきます。
平均0, 分散1の標準正規分布を作成するには、下記のようにしてあげれば出来上がります。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
incomes = np.random.normal(0, 1, 10000)
plt.hist(incomes, 50)
plt.show()色々と試して、変化を楽しんでみてください。