機械学習とは
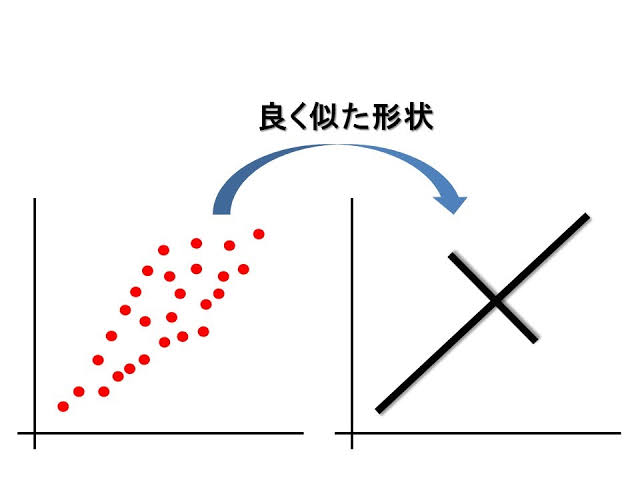
機械学習とは、データのパターンを学習することで識別や回帰による予測をソフトウェアで実現する手法です。
例えば、人の話し声を識別して文字に変換したり、有名どころだと株価の予測に使われてたりしています(実用レベルに達していない)。後は、 IoTなどと組み合わせて、オフィスや住宅の冷房・暖房最適化することで、消費電力を4割削減した実証例もあります。
機械学習では、人間には認知できない程多くの変数からパターンを学習できる。
学習のアルゴリズムは、ニューラルネットワークやサポートベクターマシーンやランダムフォレストなど多数存在する。
特徴ベクトル
識別や回帰のために観測値を順番に並べたベクトルを特徴ベクトルと言います。
例えば、体重:x1,身長:x2,体脂肪率:x3,平均的な髪の長さ:x4,毛髪面積比(ハゲ面積/頭皮面積):x5,髪の平均直径:x6 をもいいて男女を区別する場合を考えてみましょう。xを並べたものが特徴ベクトルXです。個々の要素のことは特徴量と呼びます。
X = (x1, x2, x3, x4, x5, x6)
| レコード番号 | x1 | x2 | x3 | x4 | x5 | x6 |
| 1 | 69.4 | 152.3 | 16.6 | 16.7 | 0.452 | 0.019 |
| 2 | 55.9 | 150.7 | 14.0 | 22.3 | 0.468 | 0.021 |
| 3 | 65.2 | 162.3 | 15.1 | 20.1 | 0.669 | 0.022 |
| 4 | 63.7 | 164.0 | 18.8 | 22.8 | 0.581 | 0.023 |
教師あり学習
教師あり学習とは、特徴ベクトルと正解の関係を学習する手法です。
ここで、正解が付与されたデータを教師データと呼び、そのうち学習に用いられるデータを学習データと呼びます。
| レコード番号 | x1 | x2 | x3 | x4 | x5 | x6 | y |
| 1 | 69.4 | 152.3 | 16.6 | 16.7 | 0.452 | 0.019 | man |
| 2 | 55.9 | 150.7 | 14.0 | 22.3 | 0.468 | 0.021 | man |
| 3 | 65.2 | 162.3 | 15.1 | 20.1 | 0.669 | 0.022 | man |
| 4 | 63.7 | 164.0 | 18.8 | 22.8 | 0.581 | 0.023 | woman |
教師ラベルの扱い
正解は、識別が目的の場合は文字列、回帰が目的の場合は数値となる。文字列の場合、特に正解ラベル又は教師ラベルという。
ただし、教師ラベルであっても学習時には数値に変換されて扱われている。どのように変換されるかはプログラム次第になります。
また、ソフトウェアによっては教師ラベルに数値しか受け付けないものもあり、その場合は以下のように教師ラベルを整数に変換しておく。
man -> 0、woman -> 1
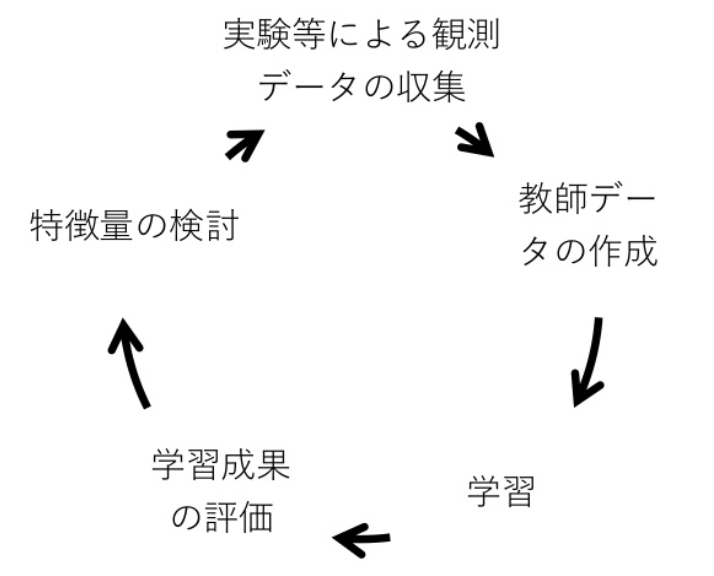
教師あり学習の作業の流れ
教師あり学習における作業の流れは以下のようになります。主成分分析は「教師データの作成」で利用されることがあります。
次元数削減の要請
機械学習では、特徴ベクトルの次元数が増えるほど、偶然生じたパターンを学習しやすくなります。これを次元の呪いと言います。
又たとえば、1つの特徴量につき3個のパターンがあるとします。それぞれのパターンが独立であれば、2次元の特徴ベクトルで生じる合計のパターン数は3の2乗で9パターンです。n次元であれば3のn乗になります。初等統計学で学ぶように、変数が正規分布と仮定すると1パターン当たりの最低限必要なデータ数は30個程です。つまり、学習データ数は30×3の乗個必要であり、次元数が増えると指数関数的に学習に要するデータ数は増加します。
必要なデータ数を確保するために実験を指数関数的に行うのは考えたくありません。実験数は少ないに越したことはありません。
したがって、特徴ベクトルの次元数は少ない方が良いです。
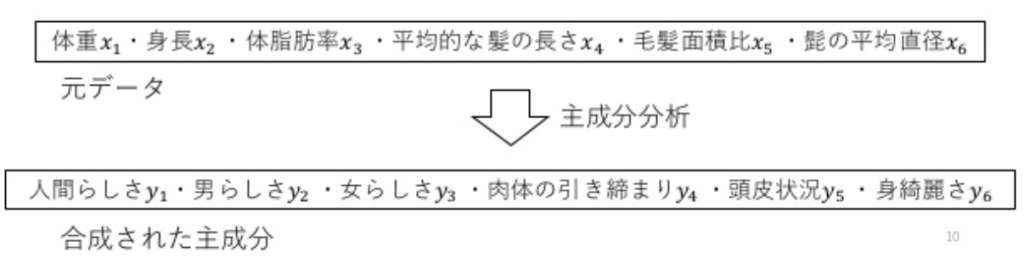
主成分分析(PCA)
主成分分析(PCA)は、次元の数を削減する「次元圧縮」や、重回帰分析の前処理として特徴量(多変量分析の世界では説明変数という)同士を無相関にする目的で利用される手法です。
PCAは、分析対象の特徴量から新たな指標を合成します。元データがn次元なら、互いに直行したn個の指標が合成される。ここで、合成された指標のことを「主成分」と呼びます。
寄与率
主成分は、それぞれの元データの情報量を分担している。情報量は、支配・影響の大きさと言い直しても良い。元のデータに対する情報量の大きさを寄与率という。又、主成分のことを寄与率の大きい順に「第一主成分」「第二主成分」という風に呼ぶ。
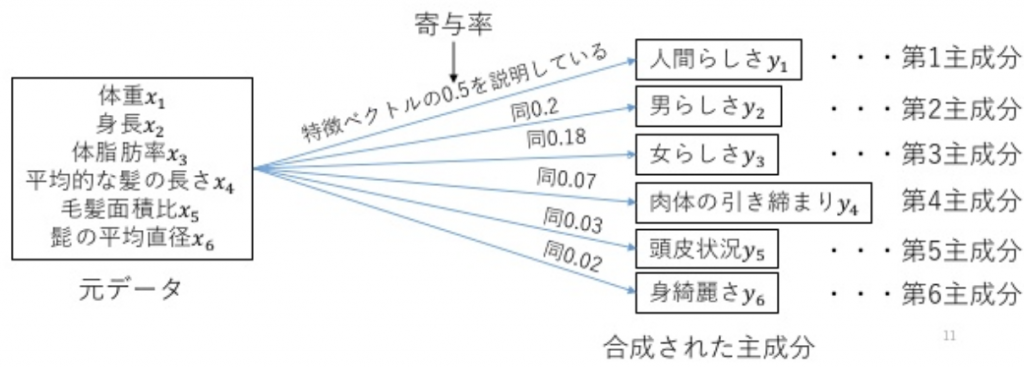
累積寄与率
寄与率を棒グラフで表示し、その積算値として累積寄与率を折れ線グラフで表示。ここで、4つ目の主成分までの寄与率の合計は0.95となっており、元データの情報の95%を第四主成分までで表現できることを示しています。
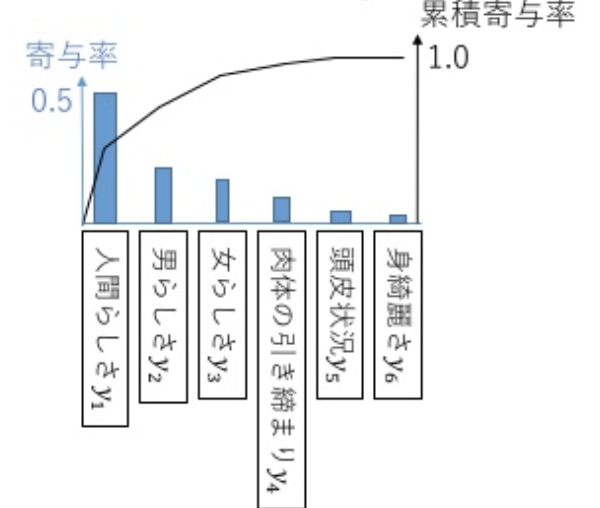
ここで、情報量の小さい主成分を捨てれば、回帰に対する計測誤差の影響を小さくできるかもしれません。
又、情報量の大きな主成分のみを学習に使えば、学習データから必要な情報が多少減ったとしても、次元数が減ったことで機械学習の総合的な性能は向上できる可能性があります。
何個の主成分を使うか
機械学習においてPCAは、次元削除のために利用される。したがって、機械学習では元データの次元数nよりも少ない主成分を用いる
データと分析の目的に依存するが、元データの90%を説明できれば、大抵の場合は上々と行った結果になります
主成分分析を伴う機械学習の作業手順
ここまでの説明で機械学習と主成分分析について何となく把握は把握はできたと思います。そこで、最後に主成分分析を伴う機械学習作業手順について整理する
- 外れ値の除去
- 元データに教師ラベルが付いていれば取り除く
- 主成分分析により、主成分得点を求める
- 累積寄与率を吟味し、第何主成分まで利用するか決める
- 主成分得点に教師ラベルを付与し、教師データを作成する
- 学習する
- 学習に用いなかった教師データを用いて学習成果を評価する
- 新たに得られた未知データを識別・予測する