前提として、共分散の定義は「2組の対応するデータ間での、平均からの偏差の積の平均値である。」というのがあります。
それを踏まえて、具体的に見ていきます。
例えば、身長と体重のデータを10人分用意したとします。
| No. | 身長(cm) | 体重(kg) |
|---|---|---|
| 1 | 111.6 | 20.1 |
| 2 | 122.5 | 24.3 |
| 3 | 123.9 | 22.7 |
| 4 | 109.2 | 15.3 |
| 5 | 115.9 | 21.8 |
| 6 | 128.3 | 23.2 |
| 7 | 115.3 | 19.1 |
| 8 | 111.4 | 12.8 |
| 9 | 121.7 | 19.7 |
| 10 | 118.6 | 16.2 |
| 平均 | 117.8 | 19.5 |
このデータを散布図にプロットして見ます。
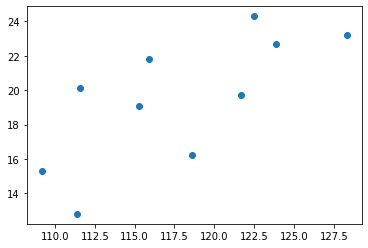
このデータは正の相関があります。
共分散の特徴として正の相関のとき共分散>0になり、負の相関のとき共分散<0になります。
実際に共分散を計算するに必要な偏差積を求めます。
偏差積の言葉通り、偏差(身長の偏差)×偏差(体重の偏差)で求めます。
偏差×偏差=(身長ー身長の平均)×(体重ー体重の平均)
これをデータ表に加えると、このようになります。
| No. | 身長(cm) | 体重(kg) | 偏差積 |
|---|---|---|---|
| 1 | 111.6 | 20.1 | -3.72 |
| 2 | 122.5 | 24.3 | 22.56 |
| 3 | 123.9 | 22.7 | 19.52 |
| 4 | 109.2 | 15.3 | 36.12 |
| 5 | 115.9 | 21.8 | -4.37 |
| 6 | 128.3 | 23.2 | 38.85 |
| 7 | 115.3 | 19.1 | 1.00 |
| 8 | 111.4 | 12.8 | 42.88 |
| 9 | 121.7 | 19.7 | 0.78 |
| 10 | 118.6 | 16.2 | -2.64 |
| 平均 | 117.8 | 19.5 |
偏差積の平均をとると共分散になります。
実際に計算すると15.1となり正の値を取ってることがわかります。
これは共分散の特徴と合致していますね。
つまり、相関の正負と共分散の正負は一致します。
もう一つ重要なこととして、共分散は単位に依存します。今回はcmとkgです。
通常は単位を記載しませんが、共分散が単位に依存しているという事実は重要です。
共分散の仕組み
もう一歩踏み込んで、正の相関があるときに共分散も正となるか見ていきます。
表の偏差積を見ると、正の値が多く直感的にも負の値よりも大きくなることが分かります。
次に象限分析を行った図を見てみます。平均の値で仕切っています。
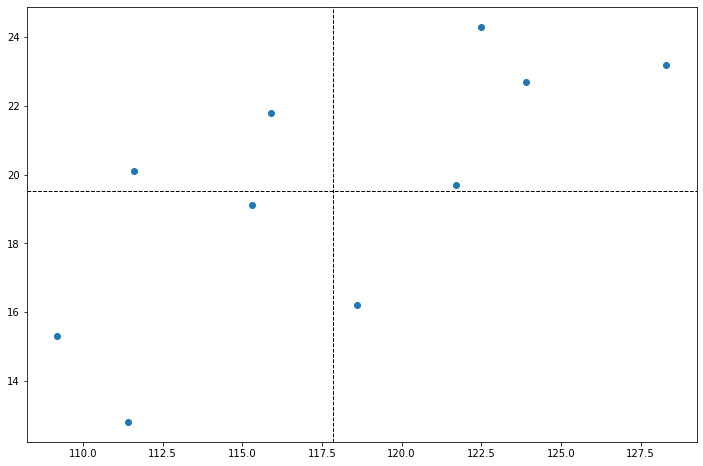
これを見ると、右上と左下の箇所は偏差積が正となります。なぜなら、偏差積を用いる共分散の定義と同じだからです。
また、交点から大きく離れている方が値が大きくなります。これらにより正の相関の時に共分散が正となります。
共分散は単位を持つので、無相関=0に近いかどうかの判断は簡単にはいきません。
そこで、単位に依存しない相関係数を用います。
相関係数=身長と体重の共分散 / (身長の標準偏差×体重の標準偏差)
分母と分子の単位が同じなので、単位は気にせず値だけ比較すれば大丈夫です。
更に分母は標準偏差なので、常に正です。相関係数の符号は分子だけで決まります。
相関係数の仕組み
相関係数は単位に依存せずに、常に「-1<=相関係数<=1」を満たす値をとります。
±1に近いほど相関が強くなります。
まとめると、「-1<=相関係数<0」は負の相関、「相関係数≒0」は無相関、「0<相関係数」は正の相関になります。